빅오란?
빅오(BigO)는 대략적으로 숫자를 세는 공식적인 표현입니다. 입력된 내용이 늘어날수록 알고리즘에 실행 시간이 어떻게 변하는지 설명하는 공식적인 방식이다.
즉, 어떤 함수의 입력 값이 늘어나거나 함수의 실행 시간이 변하는 관계 입력의 크기와 실행시간의 관계를 말한다.
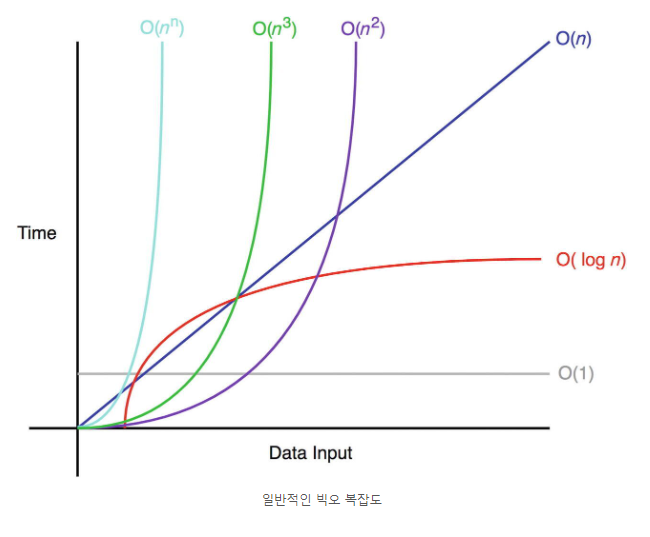
1. BigO의 예 시간 복잡도
시간 복잡도란?
입력이 커질수록 알고리즘의 실행 속도가 어떻게 바뀌는지 표현
1-1) O(1) : 상수
/*
n의 값이 늘어나도 실행 되는 시간에는 아무런 영향을 받지 않는다.
시간복잡도 O(1)
*/
function addSec(n) {
return n * (n + 1 ) / 2;
}- O(1) 상수 : n(입력값)이 커져도 실행 시간에 아무런 영향도 받지 않을 경우(항상 상수) 나타내는 표현
1-2) O(n) : 선형
/*
실행되는 시간이 n의 값이 늘어나는것과 비례하게 1:1비율로, 선형으로 늘어난다.
시간복잡도 O(n)
*/
function addFirst(n) {
var total = 0;
for (let i=0; i<=n; i++) {
total +=i;
}
return total
}- O(n) 선형 : n(입력 값)이 커질수록 실행 시간도 같이 늘어난다.
1-3) O(n^2)
/*
중첩 루프(for문)을 가진다. O(n) 연산 안에 O(n)을 가지고 있으면 O(n^2)이 된다.
시간복잡도 O(n^2)
*/
function bigO(n) {
for (let i=0; i < n; i++) {
for (let j=0; j < n; j++) {
console.log(i, j);
}
}
}- O(n^2) : 실행 시간이 n의 제곱일 경우
1-4) O(log n)
/*
입력의 크기에 따라 처리 시간이 증가하는 정렬 알고리즘에 사용 된다.
시간 복잡도 O(log n)
*/
function bigO(n) {
for (let i = 2; i <= n; i*2) {
console.log(i);
}
}
* 시간 복잡도 단순화 시키기 *
아주 큰 값을 넣는다고 가정을 한다면 나머지 값들은 의미가 없다.
- O(n + 10) = O(n)
- O(1000n + 50) = O(n)
- O(n^2 + 5n + 8) = O(n^2)
2. 배열, 객체, 내장 함수 등 시간복잡도
// 산수 O(1)
+, -, *, ...
// 값 배정 O(1)
var a = 3;
var arr = [1,2,3,4]
arr[i] // 배열 접근 O(1)
arr.push(5) // 배열 끝 추가 O(1)
arr.pop() // 배열 끝 제거 O(1)
arr.unshift(0) // 배열 앞에 추가하게 되면 모든 인덱스가 변경되기 때문에 O(n)
arr.shift() // 배열 앞에서 제거 마찬가지로 인덱스가 변경되기 때문에 O(n)
arr.slice(0,2) // O(n)
arr.concat([5,6]) // O(n)
arr.splice(2) // O(n)
arr.sort() // O(n*log n)
forEach, map, filter,reduce // O(n)
var obj = { 'name' : 'cob', 'age' : 19 }
obj['name'] // key로 객체 접근 O(1)
obj['gender'] = 'man' // 값 추가 O(1)
obj['gender'] = 'woman' // 값 변경 O(1)
delete obj['gender'] // 값 제거 O(1)
Object.keys(obj) // O(n)
Object.values(obj) // O(n)
Object.entries(obj) // O(n)
obj.hasOwnProperty('name') // O(1)
2. BigO의 예 공간 복잡도
공간 복잡도란?
입력이 커질수록 알고리즘이 얼마나 많은 공간을 차지하는지 표현
알고리즘 자체가 필요로 하는 공간을 의미한다.
시간복잡도를 생각하지 말고 공간 복잡도만 생각해야 한다.
2-1) 기본적인 규칙
- Boolean, number, undefined, null은 불변 공간으로 O(1)를 갖는다.
- reference타입, 배열, 객체 문자열은 O(n) 공간이 필요하다.
2-2) O(1) : 상수
// 입려시 이미 배열의 길이가 정해져있어 변하는것이 아니기 때문에 공간 복잡도 O(1)를 갖는다.
function sum(arr) {
let total = 0;
for (let i=0; i < arr.length; i++) {
total += arr[i];
}
}
2-3) O(n) : 선형
// arr길이 만큼 newArr의 공간이 생기기 때문에 공간 복잡도 O(n)을 갖는다.
function double(arr) {
let newArr = [];
for (let i=0; i < arr.length; i++) {
newArr.push([i]);
}
}
반응형
'CS' 카테고리의 다른 글
| 프로세스 메모리(스택, 힙, 데이터 영역, 코드 영역) 구조 개념 및 특징 (0) | 2023.01.13 |
|---|---|
| 옵저버(Observer ) 패턴 개념 및 구현 방법(Java, JavaScript) (0) | 2023.01.10 |
| 팩토리(factory) 패턴 개념 및 JavaScript에서 사용 방법 (1) | 2023.01.04 |
| 의존성 주입(DI) 개념 및 Java, JavaScript 사용 방법 (0) | 2022.12.27 |
| 싱글톤(Singleton) 패턴 개념 및 Node.js DB(MySQL, MongoDB) 연결 모듈 구현 (1) | 2022.12.26 |